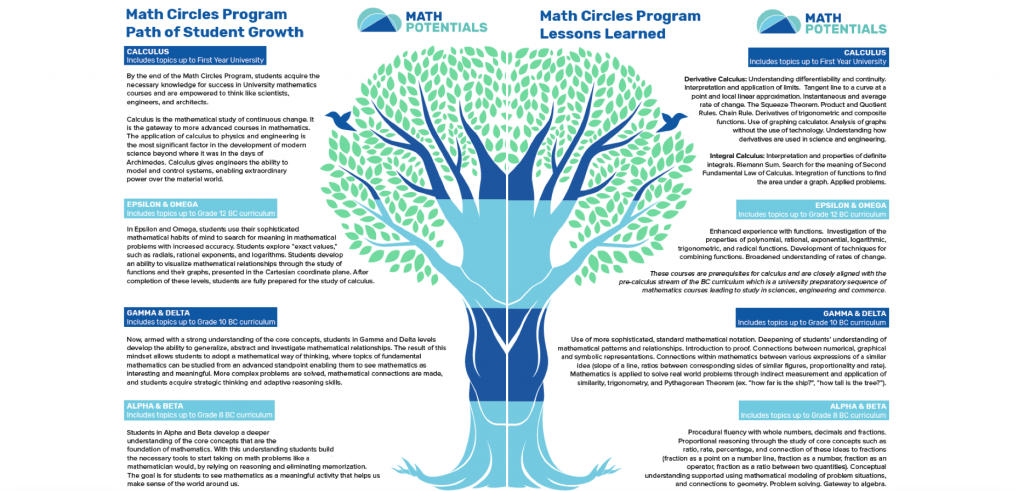
Click on the image below for a visual representation of the Path of Student Growth in the Math Circles Program.
Alpha
In Alpha class students will deepen their understanding of each topic and focus on solving challenging word problems. The curriculum draws upon Singapore Math, which aims to develop mathematical concepts for mastery. The learning process proceeds from concrete, through pictorial (models and diagrams as tools for thinking mathematically), to the abstract.
In class, students will go through a few steps to complete problems such as understanding problems, drawing diagrams to model the situations, finding answers by reasoning through a series of logical steps, presenting solutions to the class and discussing alternative solutions. Students will have many opportunities to express themselves, i.e., explaining their thinking and discussing interesting and unique ideas with their classmates.
With each topic, the student will be taught the skills to tackle problems, and for homework will be given questions of ranging difficulty.
WHOLE NUMBERS
- Place Value
- Millions
- Approximation and Estimation
- Multiplying by Tens, Hundreds, or Thousands
- Dividing by Tens, Hundreds, of Thousands
- Order of Operations
- Word Problems
MULTIPLICATION AND DIVISION BY 2-DIGIT WHOLE NUMBERS
- Multiplication
- Division
FRACTIONS
- Fraction and Division
- Addition and Subtraction of Unlike Fractions
- Addition and Subtraction of Mixed Numbers
- Product of a Fraction and a Whole Number
- Product of Fractions
- Dividing a Fraction by a Whole Number
- Word Problems
AREA OF TRIANGLE
- Finding the Area of a Triangle (through several proofs, and including obtuse triangles)
RATIO
- Finding Ratio
- Equivalent Ratios
- Comparing Three Quantities
ANGLES
- Measuring Angles
- Finding Unknown Angles
DECIMALS
- Approximation and Estimation
- Multiplication by Tens, Hundreds or Thousands
- Division by Tens, Hundreds or Thousands
- Multiplication by a 2-digit Whole Number
- Conversion of Measurements
PERCENTAGE
- Percent
- Writing Fractions as Percentages
- Percentage of a Quantity
AVERAGE
- Development of the Meaning of Average
- Word Problems
RATE
- Development of the Meaning of Average
- Word Problems
TRIANGLES
- Sum of Angles in a Triangle
- Isosceles and Equilateral Triangles
- Drawing Triangles using Compass and Straightedge
4-SIDED FIGURES
- Parallelograms, Rhombuses and Trapezoids
- Drawing Parallelograms and Rhombuses using Compass and Straightedge
VOLUME
- Cubes and Rectangular Prisms (Cuboids)
- Finding the Volume of a Solid
Beta
In Beta class students will build on their learning from the Alpha level. They will deepen their understanding of each topic and focus on solving challenging word problems. The curriculum draws upon Singapore Math, which aims to develop mathematical concepts for mastery. The learning process proceeds from concrete, through pictorial (models and diagrams as tools for thinking mathematically), to the abstract.
In class, students will go through a few steps to complete problems such as understanding problems, drawing diagrams to model the situations, finding answers by reasoning through a series of logical steps, presenting solutions to the class and discussing alternative solutions. Students will have many opportunities to express themselves, i.e., explaining their thinking and discussing interesting and unique ideas with their classmates.
With each topic, the student will be taught the skills to tackle problems, and for homework they will be given questions of ranging difficulty.
ALGEBRA
- Algebraic Expressions
- Creating Algebraic Expressions to Represent Relationships between Quantities
- Evaluating Algebraic Expressions
- Simplifying Algebraic Expressions
RATIO
- Ratio and Fraction
- Ratio and Proportion
- Changing Ratios
PERCENTAGE
- Part of a Whole as a Percentage
- One Quantity as a Percentage of Another
- Solving Percentage Problems by Unitary Method
SPEED
- Speed and Average Speed
SQUARE ROOTS AND CUBE ROOTS
- Developing the Meaning of Square Root
- Irrational Numbers
PYTHAGOREAN THEOREM
- Proving Pythagorean Theorem by Dissection – Multiple Proofs
- Applying the Theorem
- Pythagorean Triples
CIRCLES
- Radius and Diameter
- Circumference
- Area
VOLUME
- Word Problems involving Composite Solids, Displacement and Rates of Flow
SOLID FIGURES
- Surface area and volume
- Drawing Solid Figures
- Nets
- Platonic Solids
- Euler’s Theorem
Gamma
Gamma and Delta courses are a transition from the early stages of Alpha and Beta levels to more abstract yet intuitive explorations which are both “hands on” and “intellectual.” These courses are designed to entice the student into asking questions, exploring and playing with ideas, and being flexible in one’s thinking and innovative in one’s perspective. It is a course in developing the mathematical habits of mind, and it represents a perfect transition into the more formal treatment of topics that came later on.
BASE MACHINES & THE GLOBAL MATH PROJECT (EXPLODING DOTS)
- Base machines
- Arithmetic in various bases
THE COUNTING NUMBERS
- Basic laws of arithmetic, and their extension to algebra
- Ways to think about multiplication
- The roles of 0 and 1
- Geometric interpretation of expanding brackets (dimensional multiplication)
FIGURATE NUMBERS
- Square numbers
- Triangular numbers
- Relationships between figurate numbers
- Connections to algebra
FACTORS AND PRIMES
- Primes and composites
- Factors
- The infinitude of primes
- Twin primes
PARITY
- Definitions of even and odd number
- Use of these definitions in constructing simple mathematical proofs
- Applications of parity (The Gory Puzzler, Cup Turning, Path Walking)
DIVISIBILITY RULES
- Divisibility rules and their explanations (how and why they work)
- Divisibility rules are specific to our base 10 numeral system, while divisibility itself is not.
- We can use certain properties of remainders when studying divisibility rules
EUCLIDEAN ALGORITHM
- Three Related Puzzlettes
- The Euclidean Algorithm
- Key Property of Primes
FUNDAMENTAL THEOREM OF ARITHMETIC
- Prime Factorization
- The Fundamental Theorem of Arithmetic and its Proof
- Connection to the Key Property of Primes, Divisibility, and Fundamental Counting Principle (how to count the number of factors of a number, given its prime factorization)
FROM MEASUREMENT TO RATIONAL NUMBERS (2 classes)
- Meaning of fractions on a number line
- Addition and subtraction of line segments
- Multiplication and division with line segments (from area model to scale factors)
- Division of fractions explained
SCALE
- Area and scale
- Volume and scale
- Effects of scaling in the natural world
PYTHAGOREAN THEOREM
- Geometric and algebraic proofs of the theorem
- Applications of Pythagorean theorem
APPROXIMATION OF PI
- Perimeter of regular polygons
- Method of Archimedes
SOLIDS – SURFACE AREAS AND VOLUMES (2 classes)
- Cylinders, cones, and spheres
- Cavalieri’s principle
- Derivation of surface area of a sphere from its volume
TILINGS AND THE PLATONIC SOLIDS
- Tilings and tessellations
- Tilings taken to the third dimension
- Using tessellations to prove theorems
Delta
Gamma and Delta courses are a transition from the early stages of Alpha and Beta levels to more abstract yet intuitive explorations which are both “hands on” and “intellectual.” These courses are designed to entice the student into asking questions, exploring and playing with ideas, and being flexible in one’s thinking and innovative in one’s perspective. It is a course in developing the mathematical habits of mind, and it represents a perfect transition into the more formal treatment of topics that came later on.
BASE MACHINES & THE GLOBAL MATH PROJECT (EXPLODING DOTS)
- Base machines
- Arithmetic in various bases
- Negative numbers and decimal fraction
- Representing polynomials
- Operations with polynomials
LINEAR EQUATIONS AND INEQUALITIES
- Linear equations in one unknown
- Applications of linear equations in one unknown to solving of a variety of problems
- Linear inequalities in one unknown
LINEAR FUNCTIONS
- Linear function and its graph
- System of linear equations
- Applications of systems of linear equations to solving of a variety of problems
- Graphical interpretation of a system of linear inequalities in two unknowns.
- Solving of linear programming problems
SIMILARITY AND CONGRUENCE
- Parallel lines and transversals
- Basic proportionality theorem (Thales’ theorem) and its converse
- Solving problems using similarity (indirect measurement)
- Congruency theorems
GEOMETRIC CONSTRUCTIONS
- Perpendicular lines
- Copying triangles
- Copying angles
- Parallel lines
- Constructible numbers
- Construction problems
CIRCLE GEOMETRY
- Radius tangent theorem
- Two tangents theorem
- Chord theorems
- Inscribed & central angle theorem
- Applied problems in circle geometry
RATIONALS AND IRRATIONALS
- Decimals: terminating, periodic, infinite non-periodic.
- Irrational numbers and a proof that is irrational
- The geometric series
- The measure of rationals
EXPONENTS AND LOGARITHMS
- Making a slide rule and using to compute products, quotients and roots of numbers
- Powers of 2 and powers of any base
- Meaning of exponent 0, negative exponent, rational exponent, and irrational exponent
- Scientific notation
- History of logarithms and what motivated Napier to develop his logarithmic tables
- Definition of logarithms
- Properties of logarithms
- Solving exponential equations using logarithms
GROWTH AND DECAY
- Many quantities evolve according to a scheme of the form , where (growth) and (decay).
- We look at a typical crop of such problems, from population growth to carbon dating.
- Pitches in the well-tempered chromatic scale follow such a pattern with ; irrational versus rational (“Pythagorean”) musical intervals.
Epsilon
Epsilon is the natural continuation of Delta class. It continues to build the student's ability to think like a mathematician.
REVIEW OF LINEAR EQUATIONS (with some extensions)
- Solving linear equations
- Linear inequalities in one variable
- Absolute value equations in one unknown
REASONING IN MATHEMATICS *
- Inductive reasoning and conjecturing
- Deductive reasoning
- The connecting words: and, or, not
- Statements
- If…then statements
- Converse statement
- Contrapositive statement
- Direct and indirect proof
- Proof by counterexample
- Venn diagram
- Proofs of some theorems
- Word problems related to reasoning
LINEAR RELATIONS
- Division of a line segment into equal parts analytically
- Slope of a line segment, rate of change
- Graphing linear functions
- Equation of a line through two given points
- Equation of a line through the given point and with the given slope
- Different Forms of Linear Equations
- Special Cases of Linear Equations (horizontal and vertical lines)
- Equations or Parallel and Perpendicular Lines
- Linear Applications and Modelling, Distance between points and lines
SYSTEMS OF LINEAR EQUATIONS WITH TWO VARIABLES
- Linear equations with two variables
- Coordinates of a point
- Graphical representation of the linear equation with two variables, linear function
- Systems of two linear equations with two variables: graphical solution
- Solving systems of two linear equations with two variables algebraically
- Solving systems of three linear equations in three unknowns algebraically
- Word problems related to the system of linear equations
THE CIRCLE
- Theorem about central and inscribed (peripheral) angle in a circle
- Cyclic quadrilaterals
- Tangents to a circle
- Word problems related to cyclic quadrilaterals
RATIONAL FUNCTIONS AND EQUATIONS
- Graphs of Rational Functions
- Solving Rational Equations
POLYNOMIAL EQUATIONS AND FUNCTIONS
- Polynomials of 3rd and higher degree
- General shape of polynomial functions and the analysis of its end behaviour
- Reminder and factor theorems
- Word problems related to the polynomial equations and functions
QUADRATIC FUNCTIONS
- Quadratic function in general and standard form
- Domain and range of a quadratic function, zeros, maximum and minimum
- Graph of a quadratic function
- Quadratic Inequalities
- Systems of Quadratic Inequalities (including linear-quadratic inequalities)
- Word problems related to the quadratic function
FUNCTIONS
- Meaning and Notation
- Domain and Range
- Linear and Nonlinear Functions
- Inverse Function
- Composition of Functions
RADICAL FUNCTIONS AND EQUATIONS
- Graph of a Radical Functions
- Solving Radical Equations
LINEAR AND NONLINEAR INEQUALITIES
- Solving Systems of Inequalities
ELEMENTS OF TRIGONOMETRY
- Definition of trigonometric functions
- Trigonometry of a right triangle
- Values of trigonometric functions of 0°, 30°, 45°, 60°, and 90°
- Law for sine and cosine
- Word problems related to trigonometry
Omega
Omega class is based on a more "traditional mathematics" than the previous classes. Here students learn rigorous proofs and solve very difficult problems. The content is more aligned with the BC math curriculum, and will give students a strong foundation for Math 12 in high school. This course prepares students for the next level, Calculus.
TRANSFORMATION OF FUNCTIONS
- Domain and range of a function
- Translating graphs of functions
- Reflecting graphs of functions
- Stretching graphs of functions
- Combination of transformations
- Even and odd functions
EXPONENTIAL FUNCTIONS AND EQUATIONS
- Defining an exponential function
- Domain and range of an exponential function
- Graph of an exponential function
- Exponential equations
- Word problems related to exponential equations
LOGARITHMIC FUNCTIONS AND EQUATIONS
- Inverse functions
- Defining a logarithm
- Laws of logarithms
- Domain and range of a logarithmic function
- Logarithmic function and its graph
- Logarithmic equations
- Word problems solved using logarithms
TRIGONOMETRIC FUNCTIONS
- Radian measure of angles
- Angles in standard position
- Definition of trigonometric functions
- sine, cosine, tangents, and cotangents
- Values of trig. functions angles of 0°, 30°, 45°, 60°, and 90°
- (or the equivalent in radians)
- Period of a function, periods of the trigonometric functions
- Unit circle, values of trigonometric functions on the unit circle
- Graphing the sine, cosine, and tangents functions
- Graphs of trigonometric functions
- Trigonometric identities
- Trigonometric equations
ARITHMETIC AND GEOMETRIC SEQUENCES AND SERIES
- Definition of a sequence, examples
- Arithmetic sequence and series
- Geometric sequences and series
- Infinite geometric series
- Word problems related to the arithmetic and geometric sequences and series
Calculus
Calculus is the mathematical study of continuous change, and it is the gateway to more advanced courses in mathematics at the university level. The application of calculus to physics and engineering was the most significant factor in the development of modern science beyond where it was in the days of Archimedes. Calculus gives engineers the ability to model and control systems, enabling extraordinary power over the material world.
FUNCTIONS, GRAPHS, AND LIMITS REVIEW
- Review of Linear Function
- Limits (Intuitive approach)
- Use of Graphing Calculator
- Limits at Infinity; End-Behavior of a Function
LIMITS
- Limits of Rational Function
- Vertical and Horizontal Asymptotes
- Limits involving Radicals
- Questions involving Limits
CONTINUITY
- Continuity on an Interval
- Definition; Explanation of three conditions
- Continuity of Trigonometric and Inverse Trigonometric Functions
- The Squeezing Theorem
- Limit of sin(x)/x and [1-cos(x)]/x as x tends to 0
DERIVATIVES
- Derivatives
- Introduction to Derivative and its use in Science and Engineering
- Derivative defined as the limit of the difference quotient
- Understanding differentiability and continuity
- Slope of a curve at a point
THE TANGENT LINE
- Tangent line to a curve at a point and local linear approximation
- Instantaneous and average rate of change
DERIVATIVES AS FUNCTIONS
- Derivative as a Function
- Graphs of f and f ‘
- Increasing and decreasing behavior in f and f ‘
TYPES OF DERIVATIVE FUNCTIONS
- Techniques of Differentiation
- Product and Quotient Rules
- Derivatives of Trigonometric Functions
- Chain Rules, Higher Derivatives
COMPOSITE FUNCTIONS
- Derivatives of Compositions of Functions
- Generalized Derivative Formula
- Implicit and Logarithmic Differentiation
RELATED RATES
- Intermediate Value Theorem
- Mean Value Theorem
- Related Rates
INTEGRALS
- Integrals; Interpretation and Properties of Definite Integrals, Riemann Sum
- Basic Properties of Definite Integral
INTEGRALS CONTINUED
- More Integrals of Elementary Functions
- Differential Equations
APPLICATIONS OF INTEGRALS
- Applications of Integral
- Functional Rules of Calculus
SECOND FUNDAMENTAL LAW
- More problems on Second Fundamental Law of Calculus; Search for the meaning of Second Fundamental Law of Calculus
CALCULUS WITHOUT CALCULATORS
- Complete analysis of graphs and graphing without the use of technology.
APPLIED PROBLEMS
- Area and Volume problems.
Statistics
Introductory statistics involves four key topics: exploring data, planning a study, probability and statistical inference. Students will be exposed to different activities, simulations and technology use to develop strategies for collecting, organizing, analyzing, and drawing conclusions from data. There will emphasis on
effective statistical communication to prepare for written and oral analyses of real data.
Our course is based on the AP Statistics Course by College Board. Learn more here.
- One Variable Data
- Two Variable Data
- Collecting Data
- Probability, Random Variables and Probability Distributions
- Sampling Distributions
- Inference for Proportions
- Inference for Means
- Chi-Square Tests
- Linear Regression Inference